Epsilon-Delta (
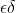
) proof is a proof of a formula on limits based on the epsilon-delta definition. Most students often have difficulties to quickly mastering the epsilon-delta definition and how to use it for proofs! Styles in proof writing usually vary greatly, and no two people will ever be expected to write exact same proof but the logical structure of any two or more proofs should be more or less the same.
In an
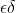
-proof, it is customary to first do some calculations to find the number
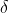
, since the proof consists of specifying a value for
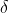
in terms of

and showing that the implication in the limit definition holds for this value of
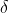
. These calculations to find
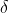
, may not necessarily be part of the proof.
Let's consider two things, before we look for an actual example:
Absolute Value
If
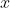
is a real number, the absolute value of
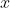
is the distance from
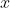
to

, written as

. We can alternatively define an absolute value of a real number
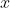
,

Therefore, if

is any real number, we have
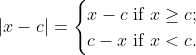
Here, we can naturally, think of
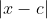
as the distance from
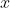
to

.
However, the following are two important equivalences involving absolute value:
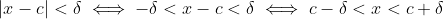
.
Here, the symbol
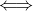
meas "is equivalent to". In words:
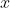
is less than
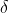
units from

if and only if the difference
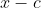
is between
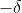
and
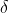
if and only if
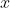
is in the interval (
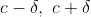
).
Epsilon-Delta Definition of a Limit
Suppose that

and
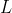
are real numbers and
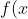)
is a function defined in an open interval containing

, except perhaps at
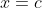
. If for every positive number
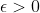
there exists a positive number
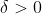
(which depends on

) such that
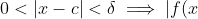 - L|< \epsilon)
,
then we say that
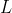
is the limit of
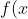)
as
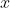
approaches

and we write
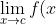 = L)
.
Intuitively, this definition says that, If
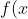)
is a function defined for all values of
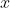
near
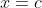
, except perhaps at
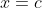
, and if
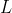
is a real number such that the values of
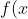)
get closer and closer to
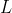
as the values of
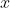
are chosen closer and closer to

, then we say
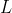
is the limit of
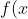)
as
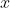
gets closer and closer to

and we write
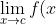 = L)
.
Example
Show that
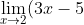 = 1) Proof
Proof
Let
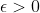
and define
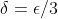
. Suppose
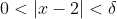
. Then, we have
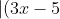 - 1| = |3x-6| = 3|x-2| < 3(\epsilon/3) = \epsilon)
(since we have made an assumption that
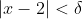
and
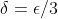
).
Therefore we have shown that
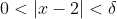
implies
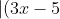 - 1|<\epsilon)
,
and by definition
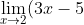 = 1)