TSSFL TECHNOLOGY STACK

Posted: **Wed Sep 28, 2016 1:45 pm**

The normal (Gaussian) distribution occurs often in nature, especially as the sample becomes large.

The probability density for the Gaussian distribution is

$$f(x, |\mu, \sigma^{2}) = \left(\sqrt{2\pi \sigma^{2}}\right)^{-1}e^{-\dfrac{(x-\mu)^{2}}{2\sigma^{2}}}$$

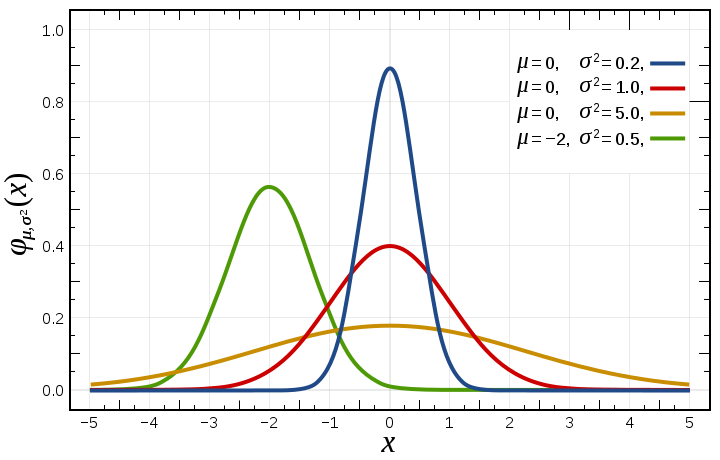
where $\mu$ is the mean and $\sigma$ the standard deviation. The square of the standard deviation, $\sigma^2$, is called the variance (see variance).

The probability density function of the normal distribution, is often called the bell curve because of its characteristic shape:

The function has its peak at the mean, and its "spread" increases with the standard deviation.

Below is the Python program that visualizes the normal distribution from 1200 random samples, with $\mu = 0, \ \sigma = 0.1$ and outputs the normal distribution curve including a histogram (see diagram below):

Code: [Select all] [Expand/Collapse]

"""Visualize normal distribution curve, including histogram"""
import numpy as np
import matplotlib.pyplot as plt
import pylab
 
mu, sigma = 0, 0.1 # mean and standard deviation
gauss = np.random.normal(mu, sigma, 1200) #Generate 1200 random samples
 
count, x, ignored = plt.hist(gauss, 60, normed=True) # x is the number of bins
plt.plot(x, 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (x - mu)**2 / (2 * sigma**2) ), linewidth=2, color='magenta', label = "mu = 0.0, sigma = 0.1")
plt.legend(loc = 1 )
plt.title("Normal Distribution")
pylab.savefig('Norm_Distr', bbox_inches='tight') #Save the plot
plt.show()

Posted: **Wed Sep 28, 2016 3:31 pm**

PDF (probability density function) for the normal distribution:

The red curve is the standard normal distribution.

What does the variance signify, from the graphs?

Posted: **Wed Sep 28, 2016 4:14 pm**

Normal distribution curve for 786432 random samples, 100 bins:

This means as sample becomes larger and larger, distribution behaves more normally!

Posted: **Thu Sep 29, 2016 7:07 pm**

More examples:

Posted: **Tue May 23, 2017 12:29 pm**

Here are a further examples of visualizing the Normal/Gaussian distributions using Python (Matplotlib and Numpy), this time is not by using random samples but from Gaussian distribution formula.

Example code1:

Code: [Select all] [Expand/Collapse]

import math
import numpy as np
import matplotlib.pyplot as plt
 
def normal(mu,sigma):
    def f(x):
        z = 1.0*(x-mu)/sigma
        e = math.e**(-0.5*z**2)
        C = math.sqrt(2*math.pi)*sigma
        return 1.0*e/C
    return f
 
X = 2
dx = 0.1
R = np.arange(-X,X+dx,dx)
 
L = list()
sdL = (0.5,1,2,3)
for sd in sdL:
    f = normal(mu=0,sigma=sd)
    L.append([f(x) for x in R])
colors = ['purple','b','r']
 
for c,P in zip(colors,L):
    plt.plot(R,P,zorder=1,color='0.2',lw=1.5)
    plt.scatter(R,P,zorder=2,s=50,color=c)
    
ax = plt.axes()
ax.set_xlim(-2.0,2.0)
#You can set y limits as well
plt.title('Normal Distribution')
plt.savefig('Normal_distribution_example.png')
plt.show()

Output:

Example code 2:

Code: [Select all] [Expand/Collapse]

import numpy as np
from scipy.stats import norm
from matplotlib import pyplot as plt
 
# You must have LaTeX installed on your system, otherwise you will get an error
# You can set usetex to False.
from astroML.plotting import setup_text_plots
setup_text_plots(fontsize=8, usetex=True)
 
#Define the distributions to be plotted
sigma_values = [0.5, 1.0, 2.0]
linestyles = ['-', '--', ':']
colors = ['r','g','purple']
mu = 0
x = np.linspace(-10, 10, 1000)
 
#Plot the distributions
fig, ax = plt.subplots(figsize=(5, 3.75))
 
for sigma, ls, c in zip(sigma_values, linestyles, colors):
    # Generate a Gaussian / Normal distribution
    dist = norm(mu, sigma)
 
    plt.plot(x, dist.pdf(x), ls=ls, color= c,lw=2,
             label=r'$\mu=%i,\ \sigma=%.1f$' % (mu, sigma))
 
plt.xlim(-5, 5)
plt.ylim(0, 0.85)
 
plt.xlabel('$x$')
plt.ylabel(r'$p(x|\mu,\sigma)$')
plt.title('Gaussian Distribution')
plt.savefig('Gauss_distr_example.png')
plt.legend()
plt.show()

Output:

or more compact plot

: Gauss_distr_example.png (21.35 KiB) Viewed 25481 times

: Gauss_distr_example.png (21.35 KiB) Viewed 25481 times

TSSFL TECHNOLOGY STACK

Visualizing random samples from a normal (Gaussian) distribution

Visualizing random samples from a normal (Gaussian) distribution

Re: Visualizing random samples from a normal (Gaussian) distribution

Re: Visualizing random samples from a normal (Gaussian) distribution

Re: Visualizing random samples from a normal (Gaussian) distribution

Re: Visualizing random samples from a normal (Gaussian) distribution