Differential Equations as Mathematical Models-Falling bodies
Posted: Tue May 12, 2015 6:11 pm
In this topic, we formulate and solve a number of differential equations that originate from real-world problems.
Example 1
A ball of mass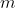 is thrown straight up from the ground with an initial velocity of
is thrown straight up from the ground with an initial velocity of 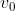 . Ignoring air resistance, find the maximum height and the time the ball takes to attain the maximum height.
. Ignoring air resistance, find the maximum height and the time the ball takes to attain the maximum height.
Solution
Let the height of the ball from the ground at any time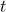 be
be 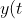) .
.
Since the force acting on the ball is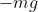 , Newton's second law of motion,
, Newton's second law of motion, 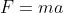 , gives the relation
, gives the relation 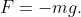
Thus
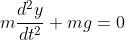
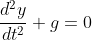
Integrating both sides,
\begin{equation}\tag{eq1}
m\dfrac{dy}{dt} + gt + c = 0
\end{equation}
Velocity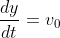 at
at 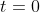 , so (eq1) yields
, so (eq1) yields
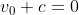 , this
, this 
Now, we have
\begin{equation}\tag{eq2} \dfrac{dy}{dt} + gt - v_{0} = 0 \end{equation}
Integrating (eq2),
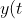 + \frac{1}{2}gt^{2} - v_{0}t + c_{1} = 0)
Since = 0, \ c_{1} = 0)
The equation of position at any time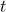 is
is
\begin{equation}\tag{eq3} y(t) = -\frac{1}{2}gt^{2} + v_{0}t \end{equation}
To find time (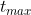 ) at the maximum height, we set the first derivative of (eq3) equals to
) at the maximum height, we set the first derivative of (eq3) equals to  (set velocity =
(set velocity =  ) to have
) to have
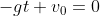 ,
, 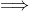
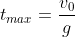 .
.
Check that the second derivative at this point is negative, i.e., = -g) .
.
Maximum height possible the ball can attain is
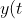_{max} = -\frac{1}{2}g\left(\dfrac{v_{0}}{g} \right)^{2} + v_{0}\left(\frac{v_{0}}{g}\right) = -\frac{1}{2}\frac{v_{0}^{2}}{g} + \frac{v_{0}^{2}}{g} = \frac{v_{0}^{2}}{2g}) .
.
Example 2
A ball weighing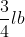 is thrown vertically upwards from a point
is thrown vertically upwards from a point  above the surface of the earth with an initial velocity of
above the surface of the earth with an initial velocity of 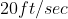 . As it rises it is acted upon by air resistance that is numerically equal to
. As it rises it is acted upon by air resistance that is numerically equal to 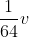 (in pounds), where
(in pounds), where  is the velocity in feet per second. How high will the ball rise?
is the velocity in feet per second. How high will the ball rise?
Solution
Let the height of the ball at at any time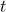 from the ground be
from the ground be 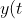) , and assume that the upward direction is positive. From Newton's second law of motion
, and assume that the upward direction is positive. From Newton's second law of motion 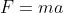 , where
, where 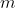 is the mass of an object and
is the mass of an object and  is acceleration due to gravity,
is acceleration due to gravity,
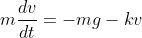 ,
, 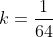
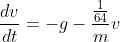
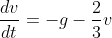
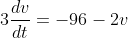
Separating variables,
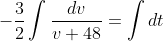
Integrating,
\begin{equation}\tag{1}-\frac{3}{2}ln(v+48) = t + c_{1} \end{equation}
Applying = 20) ,
,
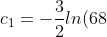)
From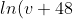 = -\frac{2t + 2c_{1}}{3})
\end{equation}\tag{2} v = e^-\left({\dfrac{2t + c_{2}}{3}}\right) - 48[/tex], where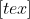 c_2 = -3ln(68) \end{equation}
c_2 = -3ln(68) \end{equation}
At the maximum height,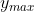 ,
, 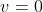
So - 48) , where
, where 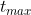 is the time the ball takes to reach maximum height.
is the time the ball takes to reach maximum height.
)
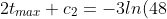)
 - 3ln(48)}{2})
Hence \begin{equation}\tag{3} y(t)_{max} = \int_{0}^{t_{max}}\left( e^-\left({\dfrac{2t + c_{2}}{3}}\right) - 48 \right)dt \ + 6 \end{equation}
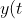_{max} = -\frac{3}{2}\left[e^-\left({\dfrac{2t + c_{2}}{3}} \right)- 48t \right]_{0}^{t_{max}} + 6)
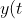_{max} = -\frac{3}{2}e^-\left( \dfrac{3(ln(68) - ln(48)) - 3ln(68)}{3} \right ) - 72\left(ln(68) - ln(48) \right) - \left( -\frac{3}{2}e^-{\left(-ln(68) \right)}\right) + 6)
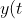_{max} = -\frac{3}{2}e^{ln(48)} - 72\left(ln(68) - ln(48) \right) + \frac{3}{2}e^{ln(68)} + 6)
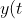_{max} = -72 + 102 - 72\left(ln(68) - ln(48) \right) + 6 = 10.92191801 ft.)
To be continued.
Example 1
A ball of mass
Solution
Let the height of the ball from the ground at any time
Since the force acting on the ball is
Thus
Integrating both sides,
\begin{equation}\tag{eq1}
m\dfrac{dy}{dt} + gt + c = 0
\end{equation}
Velocity
Now, we have
\begin{equation}\tag{eq2} \dfrac{dy}{dt} + gt - v_{0} = 0 \end{equation}
Integrating (eq2),
Since
The equation of position at any time
\begin{equation}\tag{eq3} y(t) = -\frac{1}{2}gt^{2} + v_{0}t \end{equation}
To find time (
Check that the second derivative at this point is negative, i.e.,
Maximum height possible the ball can attain is
Example 2
A ball weighing
Solution
Let the height of the ball at at any time
Separating variables,
Integrating,
\begin{equation}\tag{1}-\frac{3}{2}ln(v+48) = t + c_{1} \end{equation}
Applying
From
\end{equation}\tag{2} v = e^-\left({\dfrac{2t + c_{2}}{3}}\right) - 48[/tex], where
At the maximum height,
So
Hence \begin{equation}\tag{3} y(t)_{max} = \int_{0}^{t_{max}}\left( e^-\left({\dfrac{2t + c_{2}}{3}}\right) - 48 \right)dt \ + 6 \end{equation}
To be continued.