Intersection of two ideals of a ring R

[John Linus B,]

Qn. Show that the intersection of two ideals of a ring R is an ideal

[Heslon]

Try this link to get an idea:

http://www-history.mcs.st-and.ac.uk/~jo ... ls/T4.html

[Eli]

Let me define what is ring and ideal in abstract algebra context.

A ring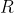 is a set with two binary operations of and . , such that:

(i) is an abelian group,

(ii)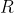 is closed under multiplication and ,

(iii) .

Usually, there is left ideal, right ideal and 2-sided ideal, but, here we mean 2-sided.

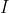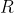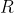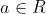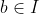A subset of a ring is called an ideal provided it is a subgroup of the additive group and if and then:

(i) ,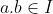

(ii) ,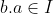

(iii) .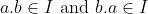

Hope this will give others a highlight and a hint to answer the question!