Data Representation and Visualization: From Scatter Plot to 2-Dimensional Histogram to Contours

[Eli]

Appropriate representation of data is a key point in data analysis. Hundreds to thousands of numerical data points, for example, can be difficult to interpret unless correctly visualized. Improper choice of visualization can however lead to overplotting and make the figure hard to read and impossible to determine how many data points are in each position. We emphasize that, a proper means of data visualization must be chosen for a sensible data interpretation.

In this post, we present various multivariate data visualization techniques using Python programming language and show how different choices of data visualization can progressively improve its representation and interpretation.

It is important to acquaint yourself with multinormal or multivariate Gaussian distribution if you haven't done so.

The general approach to generate/draw random samples from a multivariate normal distribution in Python is by using multivariate_normal function,

sample = multivariate_normal(mean, covariance, options), see random sampling at Scipy.org.

1. Scatter Plot

A scatter plot traditionally displays the value of 2 sets of data on 2 dimensions - xy plane, where each data point represents an observation. Scatter plot is useful to study the relationship between variables. We can use different colors or/and shapes for data points (dots) illustration. 2-dimensional scatter point can be extended to 3-dimensional scatter plot by adding one more dimension or plot what is called bubble plot, where the third dimension or the values of an additional variable are represented by the size of the dots. It is obvious that too many bubbles make the chart hard to read, so bubble plotting is usually not recommended for big amount of data.

Below is a piece of code to produce a scatter plot from 200 multivariate normal distribution randomly generated data points.

Code: [Select all] [Expand/Collapse]

1. # Import required libraries
2. import numpy as np
3. import matplotlib.pyplot as plt
4. from scipy.stats import kde
5.  
6. #Create 200 data points
7. data = np.random.multivariate_normal([0, 0], [[1, 0.5], [0.5, 3]], (200,))
8. x, y = data.T #Shape = (200, 200)
9.  
10. fig  = plt.subplot(111, aspect='auto') #choose 'equal' if you want
11. plt.title("Scatter Plot")
12. fig.plot(x, y, 'o', markersize=7, color='black', alpha=1.0, label="Scatter")
13. plt.legend(loc=1)
14. plt.savefig('scatter_plot.png', bbox_inches='tight') #Save the plot
15. plt.show()

The scatter plot output is



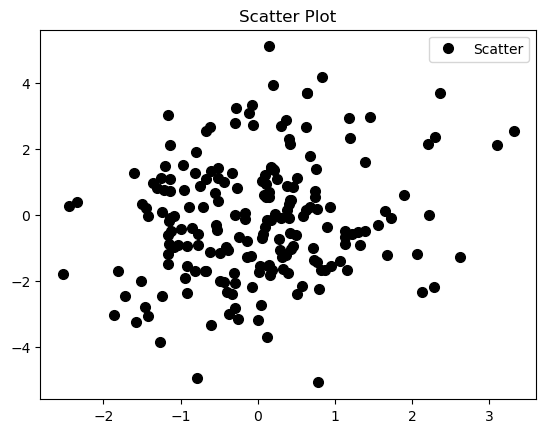
As suggested before, there is a lot of over plotting in the scatter plot that makes it hard to read, even worse if we are dealing with larger random samples.

2. Histogram

An histogram is a graphical representation of the distribution of numerical data, where the input is one numerical variable only. The variable is split into several bins, and the number of observations in each bin is represented by the height of the bar. Be aware that the shape of the histogram is greatly determined by the number of bins you set.

You can decide to represent your data by using a simple histogram that is produced by just the few lines of code below (see a method that gives you more control in creating histograms for multiple datasets and compare their distributions on the same axes, in our case, the datasets represented by variables x and y above, ):

Code: [Select all] [Expand/Collapse]

1. data = np.random.multivariate_normal([0, 0], [[1, 0.5], [0.5, 3]], (200,))
2. plt.title("Histogram")
3. plt.hist(data, bins = 5, facecolor = 'lightblue', alpha = 1.0) #Here the number of bins = 5
4. plt.savefig('https://github.com/TSSFL/figures/blob/master/histogram.png', bbox_inches='tight')

which will result to



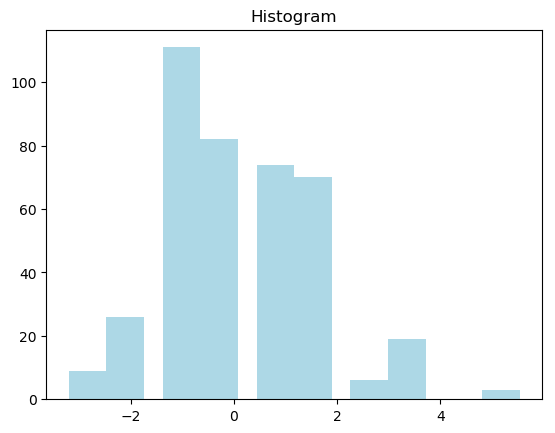
Histogram may however be not a good choice in most cases.

3. Hexbin or 2-D Histogram

We can improve our solution by cutting the plotting window into several bins, and represent the number of data points in each bin by a color.

A 2-D histogram or a 2-D density is an extension of the well known histogram. It shows the distribution of values in a data set across the range of two quantitative variables. For too many data points, the 2-D density plot counts the number of observations within a particular area of the 2-D space. Depending on the shape of the bin, this specific area can be a square or a hexagon (hexbin), hence, resulting in Hexbin plot or 2-D histogram.

A 2-D histogram is simple and easy to understand, it fundamentally a blocky plot.

We can achieve a hexbin plot through the following lines of code:

Code: [Select all] [Expand/Collapse]

1. #Split the plotting window into 20 hexbins
2. nbins = 20
3. plt.title('Hexbin')
4. plt.hexbin(x, y, gridsize=nbins, cmap=plt.cm.BuGn_r)
5. plt.savefig('https://github.com/TSSFL/figures/blob/master/hexbins.png', bbox_inches='tight')
6. plt.show()

The resulting hexbin is



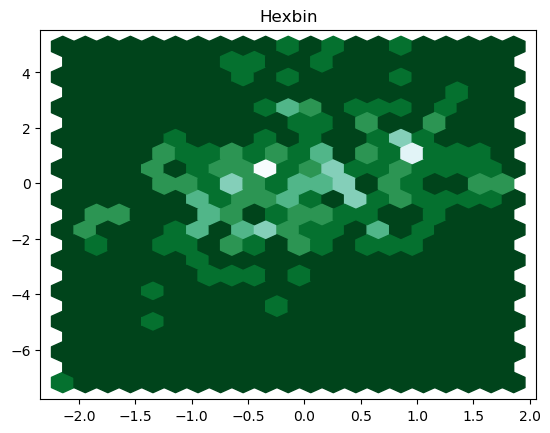
We can as well plot a 2-D histogram by using the following piece of code:

Code: [Select all] [Expand/Collapse]

1. plt.title('2-D Histogram')
2. plt.hist2d(x, y, bins=nbins, cmap=plt.cm.BuGn_r)
3. plt.savefig('https://github.com/TSSFL/figures/blob/master/two_D_histogram.png', bbox_inches='tight')

Resulting 2-D histogram is




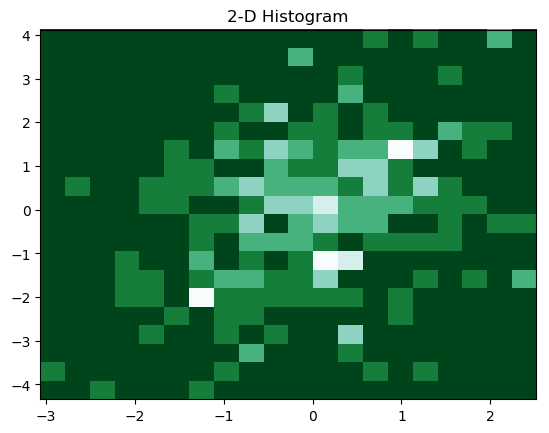
5. Gaussian Kernel-Density Estimate (KDE)

We can smooth a 2-D histogram (2-D density plot) to make a kernel-density estimate (KDE). Instead of a point falling into a particular bin, it adds a weight to surrounding bins, usually in a bell-shaped curve "Gaussian distribution". There is no one correct way of plotting Gaussian KDE, you need to be more careful to get the correctly statistically interpretable Gaussian KDE plot. Gaussian KDE is basically a 2-D density plot.

This piece of code

Code: [Select all] [Expand/Collapse]

1. #Evaluate a Gaussian KDE  on a regular grid of nbins x nbins over data extents
2. k = kde.gaussian_kde(data.T)
3. xi, yi = np.mgrid[x.min():x.max():nbins*1j, y.min():y.max():nbins*1j]
4. zi = k(np.vstack([xi.flatten(), yi.flatten()]))
5.  
6. #Plot a density-estimate
7. plt.title('Gaussian KDE')
8. plt.pcolormesh(xi, yi, zi.reshape(xi.shape), cmap=plt.cm.BuGn_r)
9. plt.savefig('https://github.com/TSSFL/figures/blob/master/Gaussian_KDE.png', bbox_inches='tight')

produces the Gaussian KDE figure below.



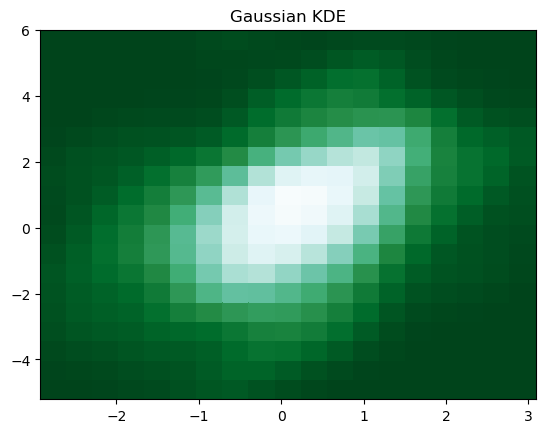
6. 2-D Density with Shading

We can add shading to 2-D density plot using the below piece of code

Code: [Select all] [Expand/Collapse]

1. plt.title('2-D Density with Shading')
2. plt.pcolormesh(xi, yi, zi.reshape(xi.shape), shading='gouraud', cmap=plt.cm.BuGn_r)
3. plt.savefig('https://github.com/TSSFL/figures/blob/master/Shaded_2_D_Density.png', bbox_inches='tight')

to have the plot



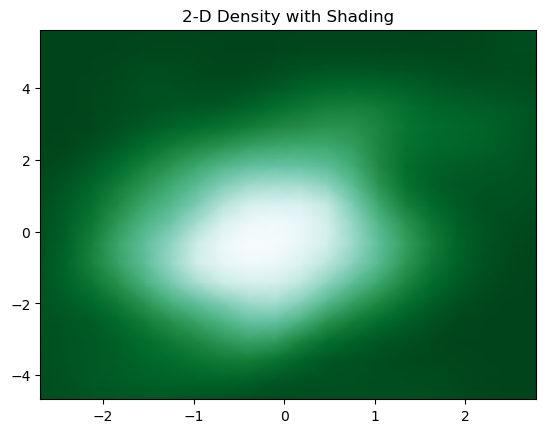
7. Adding Contours

We can finally add contours in a 2-D density to denote each step using the code

Code: [Select all] [Expand/Collapse]

1. #Add contours
2. plt.title('Contour')
3. plot.pcolormesh(xi, yi, zi.reshape(xi.shape), shading='gouraud', cmap=plt.cm.BuGn_r)
4. plot.contour(xi, yi, zi.reshape(xi.shape) )
5. plt.savefig('https://github.com/TSSFL/figures/blob/master/Contours.png', bbox_inches='tight')

The resulting contour plot is



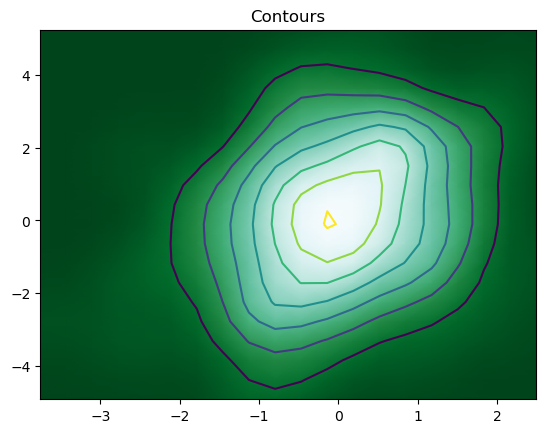
But, the most convenient and efficient way is to plot these figures altogether. We can achieve this by combining all the code snippets and creating a figure with 7 subplots and use axes to plot figures in their respective positions:

fig, axes = plt.subplots(ncols=6, nrows=1, figsize=(25, 6))

The whole code is

Code: [Select all] [Expand/Collapse]

1. """From scatter to contour plot"""
2. #Import required libraries
3. import numpy as np
4. import matplotlib.pyplot as plt
5. from scipy.stats import kde
6.  
7. #Create 200 data points
8. data = np.random.multivariate_normal([0, 0], [[1, 0.5], [0.5, 3]], (200,))
9. x, y = data.T
10.  
11. #Create a figure with 7 plot grids
12. fig, axes = plt.subplots(ncols=7, nrows=1, figsize=(25, 5))
13.  
14. #Scatter plot, see that there is a lot of over plotting here
15. axes[0].set_title('Scatter Plot')
16. axes[0].plot(x, y, 'o', markersize=7, color='black', alpha=1.0, label="Scatter")
17.  
18. #Plot Histogram
19. axes[1].set_title("Histogram")
20. axes[1].hist(data, bins = 5, facecolor = 'green', alpha = 0.6) #Here the number of bins = 5
21.  
22. #Split the plotting window into several hexbins
23. nbins = 20
24. axes[2].set_title('Hexbin')
25. axes[2].hexbin(x, y, gridsize=nbins, cmap=plt.cm.BuGn_r)
26.  
27. #Plot 2-D Histogram
28. nbins = 20
29. axes[3].set_title('2-D Histogram')
30. axes[3].hist2d(x, y, bins=nbins, cmap=plt.cm.BuGn_r)
31.  
32. #Plot a Gaussian KDE on a regular grid of nbins x nbins over data extents
33. nbins = 20
34. k = kde.gaussian_kde(data.T)
35. xi, yi = np.mgrid[x.min():x.max():nbins*1j, y.min():y.max():nbins*1j]
36. zi = k(np.vstack([xi.flatten(), yi.flatten()]))
37.  
38. #Plot a Density
39. axes[4].set_title('Gaussian KDE')
40. axes[4].pcolormesh(xi, yi, zi.reshape(xi.shape), cmap=plt.cm.BuGn_r)
41.  
42. #Add shading 2-D Density
43. axes[5].set_title('2-D Density with Shading')
44. axes[5].pcolormesh(xi, yi, zi.reshape(xi.shape), shading='gouraud', cmap=plt.cm.BuGn_r)
45.  
46. #Add Contours
47. axes[6].set_title('Contours')
48. axes[6].pcolormesh(xi, yi, zi.reshape(xi.shape), shading='gouraud', cmap=plt.cm.BuGn_r)
49. axes[6].contour(xi, yi, zi.reshape(xi.shape) )
50. plt.savefig('plots.png', bbox_inches='tight')

The output figure is



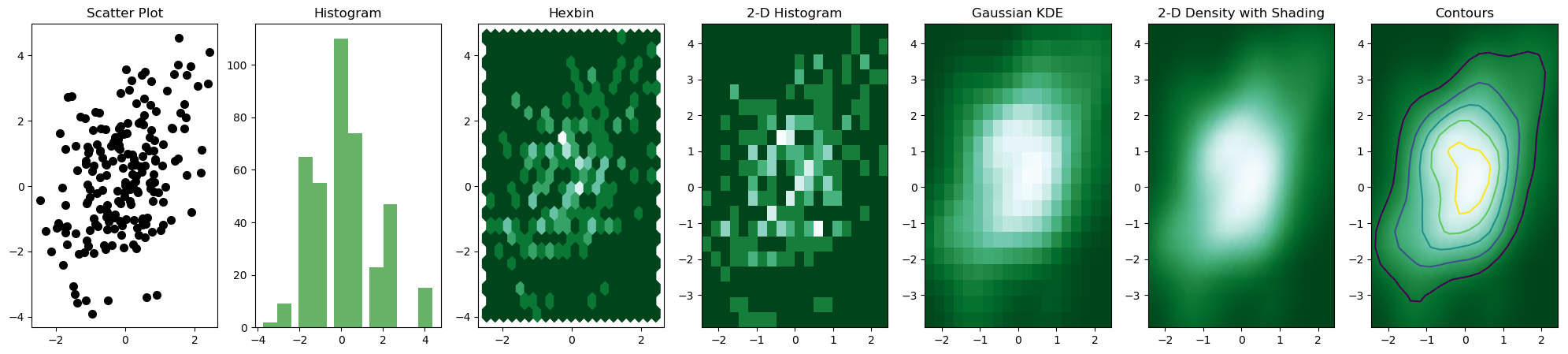
Note that it is important to use np.random.seed() to ensure consistency in random sample generation during each runtime.

[Joseph Bundala]

This is interesting @Eli
I have been wondering about random numbers for quite sometimes now. However, i would like to know if i generate random numbers at the first iteration of two different programming languages will they be the same values?
Octave

Code: [Select all] [Expand/Collapse]

1. m = rand(3,2)
2. m =
3.    0.64412   0.46867
4.    0.61134   0.34645
5.    0.23313   0.73981

[Eli]

@Simulink

Properties of random numbers, make it impossible to generate the same values with different programming languages, even by re-executing the same calculations using the same language. It can only coincidentally happen you get similar output but this behavior is generally not expected, unless you impose some constraints/restrictions.

Here is an example in Octave:

Code: [Select all] [Expand/Collapse]

1. %Standard Normal Distribution
2. >> x = randn(1,3)
3. x =  0.9206277  -0.0065868   2.4576254
4.  
5. >> y = randn(1,3)
6. y = 0.27826   1.87643  -0.77047
7.  
8. >> z = randn(1,3)
9. z = -2.0805   2.2641   1.1767
10.  
11. %Uniform Distribution  
12. >> x = rand(1,3)
13. x =  0.91030   0.38032   0.11765
14.  
15. >> y = rand(1,3)
16. y = 0.93542   0.91611   0.87546
17.  
18. >> z = rand(1,3)
19. z = 0.479022   0.429005   0.022451
20.  
21. %Uniform distribution of integers
22.  
23. >> x = randi(9, 4)
24. x =   2   4   1   4
25.       5   3   5   6
26.       2   2   9   5
27.       5   8   3   5
28.  
29. >> y = randi(9, 4)
30. y =   3   9   6   7
31.       5   2   8   8
32.       9   7   5   2
33.       7   5   7   6
34.  
35. >> z = randi(9, 4)
36. z =   5   8   3   3
37.       9   1   9   4
38.       9   2   3   3
39.       2   4   9   5

Random numbers play an important role in statistical analysis and probability theory. Random numbers have two important conditions to meet:

1. The values must be drawn from a uniform distribution over a defined interval or set;

2. it should be impossible to predict any future values based on the past or present ones. This means such numbers are required to be independent, so that there are no correlations between successive numbers in the sequence. In simple terms, Random means no biasing or no way of knowing the outcome.

Random numbers are sampled from a set where drawing each element is equally probable, and the set which meets this condition is almost, always uniform distribution. The uniform distribution property gives equal probability/chance for the occurrence of unpredictable values. For a sequence of numbers to be random, it requires that the frequency of the occurrence of these random numbers to be approximately the same. In other words, if we specify a large sample of random numbers we can reproduce a uniform distribution.

Uniform distribution is different from such distributions as normal, since for normal distribution, numbers close to the mean are much more likely to be favored than those far away from the mean. Uniformly distributed random numbers on an interval have equal probability of being selected or happening while normally distributed numbers on an interval have probabilities that follow the normal distribution pattern -- a bell-shaped curve.

"It is impossible to produce an arbitrarily long string of random digits and prove it is random", reference http://mathworld.wolfram.com/RandomNumber.html

We use the following Python code to illustrate the explanations.

Code: [Select all] [Expand/Collapse]

1. import numpy as np
2. import matplotlib.pyplot as plt
3.  
4. #Uniform distribution
5. uniform_distr = np.random.uniform(-4, 4,1000)
6. count, bins, ignored = plt.hist(uniform_distr, 30, density=True)
7. plt.plot(bins, np.ones_like(bins)*0.1, linewidth=2, color='orange', label ="Probability")
8.  
9. #Normal distribution
10. mu, sigma = 0, 1.0
11. normal_distr = np.random.normal(mu, sigma, 1000)
12. count, bins, ignored = plt.hist(normal_distr, 30, density=True, color="green", alpha=0.5)
13. #Try plt.hist(x, bins, density=1, histtype='bar', rwidth=0.8)
14. plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi))*np.exp( - (bins - mu)**2 /
15. (2 * sigma**2) ),linewidth=2, color='purple', label="Normal distribution")
16. plt.title("Uniform and Normal Distributions")
17. plt.legend()

Here are the results from the code.

1. Uniform distribution

A random sample tends to exhibit the same properties as the population from which it is drawn (see #3).



2. Normal distribution




3. If we specify a large sample of random numbers we can reproduce a uniform distribution:



4. Uniform and normal distributions



The blue bars shows a uniform distribution over the range [-4, 4] and the orange line shows that each number under uniform distribution is equally probable - uniformly likely to be picked.

The purple line shows a normal distribution with mean of 0 and standard deviation of 1.0. This suggests that numbers close to the mean are more likely to be picked than those far away from the mean.

[Joseph Bundala]

Well explained @Eli , that's why you had a python function to keep the consistency in the data generated at each run. I doubt if Octave has built in functions like KDE, multivariate Gaussian unless loaded. However, i think Matlab has them and Python is a full package kind of a thing. Still learning these powerful tools and gonna check for Hexbins as well in future.

Octave

Code: [Select all] [Expand/Collapse]

1. clc
2. clear all
3.  
4. % statistics and econometrics  packages
5. pkg load statistics                
6. pkg load econometrics        
7. %pkg load nan
8.  
9. sigma = [1, 0.5; 0.5, 3];     % covariance matrix
10. mu = [0, 0];                    % mean
11. N = 200;                         % N- random numbers
12. data = mvnrnd (mu, sigma, N); % multivariate normal distribution
13. x = data(:,1);
14. y = data(:,2);
15.  
16. figure 1
17.  
18. h(1) = subplot(2,3,1);
19. h(2) = subplot(2,3,2);
20. h(3) = subplot(2,3,3);
21.  
22. set(h(1),'NextPlot','add');
23. set(h(2),'NextPlot','add');
24. set(h(3),'NextPlot','add');
25.  
26. %scatter plot
27. scatter(h(1),x,y,'o')
28. title("Scatter")
29.  
30. %Histogram 5 bins
31. nbins = 5;
32. hist (h(2),data, nbins);
33. title("Histogram");
34.  
35. %contour data
36. %Kernel density estimator
37. [bandwidth, density, xi, yi] = kde2d(data);
38. contour(h(3),xi ,yi ,density,5)
39. axis([-3 3 -4 4]);
40. title("Contour")
41. saveas(1,"contour.jpg")

[Eli]

A random variable should be contrasted from the traditional mathematical or algebraic notations used to represent quantities. The idea of random variables originates from random processes (for example some experiment) that map outcomes to numbers, such that a random variable is a set of all possible values (sample space) from a random/unbiased experiment. Generally, a random variable is associated with uncertainty, to the extent we can't fully know or tell in advance what the value or outcome will be. A random variable is assumed to follow some probability distribution, which is usually the case in practice. A random variable is often denoted by a capital letter, such as X, Z, or Y; and can be discrete or continuous.

What do you think?

[Eli]

What are the meanings of a stochastic process, expected value, and ensemble average?

[Eli]

In post #3, I encountered Error:AttributeError ： ‘Rectangle’ object has no property ‘normed’
Reason: The normed parameter is no longer used, I have replaced it by density.