Calculus: Integration

[Eli]

The integration problem below was submitted by a student who needs help to solve it.

Can you solve the problem?

Here it is:

Prove that \(\large

\begin{align} \int_0^1 \sqrt{\frac{\log(1/t)}{t}} \,\mathrm{d}t = \sqrt{2\pi} \end{align}\)

[Joseph Bundala]

Assumptions:
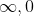A()=A(), where A is the area under the curve.

Knowledge:
Integration by substitution,
Integration by parts,
There is Gauss error function that i used, if there are some other methods then someone else may share them as well. This function will help us to 'end' the integration whenever we reach to integrate such function below, we will substitute with 'erf' function.



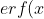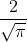
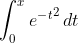
Note: erf has standard values for zero and infinity, the values can be proved in matlab console, type erf(0) and erf(1/0)
=
=

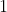
The procedure:
In case of errors, then suggestions are open. May be mods will try to put this in a good mathematical typesetting.