To prove that a binary operation on a certain set, say
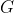
makes it a group, we need to show that four properties are satisfied. Let's illustrate this by examples.
Problem 1
Let
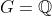
be a set of non-zero rational numbers such that
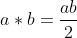
,
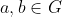
. Show that
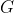
is a group.
(i) Closure: If

and
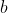
are non-zeros, then
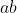
is non-zero rational number, and so
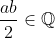
(ii) Associative: For
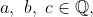
 = a*\left(\frac{bc}{2} \right) = \frac{ a\left(\frac{bc}{2} \right)}{2} = \frac{a(bc)}{4})
Similarly,
*c = \left(\frac{ab}{2} \right)*c = \frac{\left(\left(\frac{ab}{2} \right) c\right)}{2} = \frac{(ab)c}{4})
(iii) Identity element: The number two acts as the multiplicative identity, so,
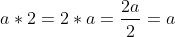
(iv) Inverse: If

is non-zero, then
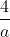
is a no-zero rational number and serves as the multiplicative inverse of

, since
*a = \frac{4a}{2a} = 2) Problem 2
Problem 2
Let
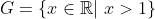
, i.e., the set of all real numbers greater than
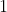
. Define
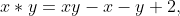
for
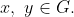
Show that the operation

makes
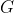
a group.
Solution
For
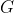
to be a group, four properties: closure, associative, identity element and inverse must be satisfied.
(i) Closure: If
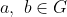
, then
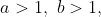
so
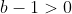
and therefore multiplying

by
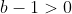
both sides, it follows immediately that
>(b-1) \ \implies ab - a - b>-1 \ \implies ab-a-b+1>0 \\ \\ \implies ab-a-b+2>1.)
Hence the operation

is closed on
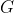
.
(ii) Associative: For
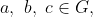
we have
 = a*(bc-b-c + 2) \\ \\ = a(bc-b-c+2)-a-(bc-b-c+2)+2 \\ \\ = abc - ab - ac - bc + a + b + c)
On the other hand, we have
*c = (ab - a - b +2)*c \\ \\ = (ab-a-b+2)c - (ab-a-b+2) - c + 2 \\ \\ = abc - ab - ac - bc + a+ b+c)
Thus
 = (a*b)*c.)
(iii) Identity:
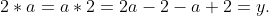
Hence, 2 is the identity element for the operation

.
(iv) Inverse: Given any
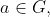
we need to solve the equation
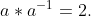
This gives the equation
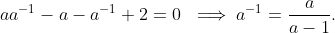
This solution belongs to
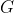
since
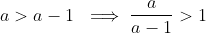
NB: You can also check that
 = \frac{a^2}{a-1} - a - \frac{a}{a-1} + 2 = \frac{a^2 - a^2 + a - a}{a-1} + 2 = 2.)